Lecture 9
Machine Learning and Neural Networks
$$
$$
Motivation
In the previous lecture, we viewed different priors or regularizers and how they can be used to help solve inverse problems. A regularizer for least squares in the most general sense is given as:
\[ \min_{u} \left\{ \frac{1}{2} \left\| Au(x) - b \right\|_2^2 + \lambda R(u) \right\} \]
where \(u(x)\) is a distribution of the unknowns over the domain \(x\), \(A\) is the forward operator, \(b\) is the data, and \(R(u)\) is the regularizer. A neural network can be used as a universal approximator for the function \(R: \mathbb{R}^n \rightarrow \mathbb{R}\), where \(n\) is the number of unknowns, or values of \(u\).
Neural Networks
A Basic Neural Network: Single-Layer Perceptron (SLP)
A basic neural network will have parameters \(\theta\) that can be trained or learned, along with the input, \(u\).
\[y = R(u; \theta) = w^T \sigma(Wu+a), \quad \theta := \{w, W, a\}\]
The function \(R\) in this case is a function defined for fixed \(\theta\). The term \(\sigma\) is a non-linear activation function, of which there are many choices.
\(u\): Input vector to the neural network.
\(y\): Output of the neural network, parameterized by \(\theta\), representing the learned function.
\(\theta := \{w, W, a\}\): Set of trainable parameters in the network, where:
- \(w\): Weight vector for the output layer
- \(W\): Weights matrix for the hidden layer
- \(a\): Bias vector added to the hidden layer
\(\sigma\): Non-linear activation function applied element-wise to the affine transformation \(Wu + a\).
So a single layer neural network can be seen as the affine transformation of the vector \(u\) followed by a non-linear activation function and a weighting metric for the resultant vector.
This can be used as an approximator for the true regularizer \(R(u) \approx R_T(u)\) in the inverse problem.
Suppose that we have a known set of mappings \(u_i \rightarrow y_i\), where \(i = 1, \ldots, N\). For example we might have some information about the regularizer \(R(u)\) for a set of \(u\) values. One possible technique is to train an SLP to approximate the true regularizer \(R_T(u)\).
The function \(y = R(u; \theta)\) returns a scalar, taking its transpose will not change the output:
\[y = w^T \sigma(Wu+a) = \sigma(u^TW + a)w\]
Then using the squared loss function, we can define the loss function as:
\[\mathcal{L}(\theta) = \frac{1}{2} \sum_{i=1}^N \left \| \sigma(u^TW + a)w - y_i \right \|^2\]
The summation is reorganized to get rid of the summation term where \(U\) is a matrix with the \(u_i^T\) as the columns, A is a matrix with \(a\) as the columns, and \(y\) is the vector of \(y_i\) values.
\[\mathcal{L}(\theta) = \frac{1}{2} \left \| \sigma(U^TW + A)w - y \right \|^2\]
For simplicity of this analysis, we can assume without loss of generality for the problem at hand that \(A = 0\) and \(\sigma\) is the identity operator. Then:
\[\hat\theta = \min_{\theta} \mathcal{L}(\theta) = \min_{\hat w} \frac{1}{2} \left \| U^T\hat w - y \right \|^2.\]
where \(\hat w = Ww\).
Non-linearity Analysis
This least squares problem will generally be ill-posed when the activation function is not present (the case with identity activation). \(N>d\) means that there are more equations than there are unknowns, because \(\hat w\) is of dimension \(d\), so there could be infinite solutions.
\[\hat{\theta} = \min_{\theta} \frac{1}{2} \left\| \underbrace{ \begin{bmatrix} \ & \ & \ \\ \ & U^T & \ \\ \ & \ & \ \\ \end{bmatrix} }_{N \times d} \cdot \underbrace{ \begin{bmatrix} \ & \ & \ \\ \ & W & \ \\ \ & \ & \ \\ \end{bmatrix} }_{N \times k} - y \right\|^2 \]
Idea 1:
If we can increase the rank of the \(Z = U^TW\) matrix, then perhaps it is possible to solve the problem batter. We select for there to be a larger weights matrix \(W\) that is \(N \times m\) where \(m > d\). In the resulting \(z = U^TW\) matrix, the rank will still be \(\text{rank}(Z) \le d\).
Idea 2:
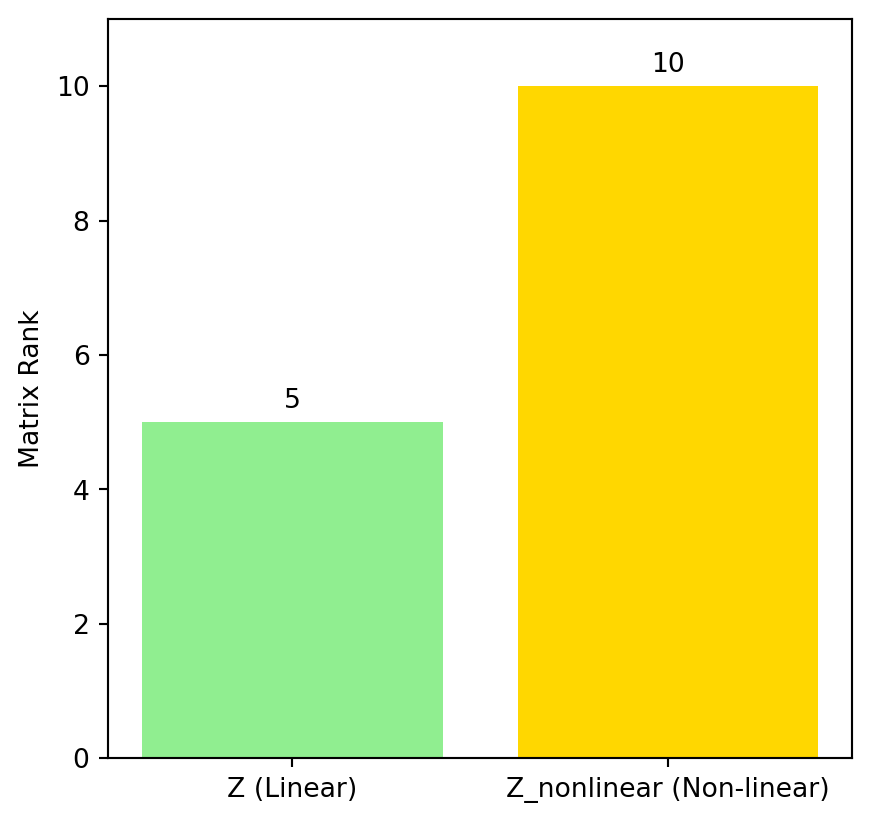
Use a non-linear activation function \(\sigma\) that operates element-wise on the matrix \(Z = U^TW\) to increase the rank of the matrix so that \(\text{rank}(\sigma(Z)) = \min (N,m)\).
In practice the exact activation function is not important. It may be the case that \(\text{rank}(\sigma(Z)) = 3\) for example, but applying the activation function will increase the rank to the minimum dimension size of the weights matrix \(W\). This can give a unique solution the least squares problem.
\[ \hat{\theta} = \min_{\theta} \frac{1}{2} \left\| \sigma \left( \underbrace{ \begin{bmatrix} \ & \ & \ \\ \ & U^T & \ \\ \ & \ & \ \\ \end{bmatrix} }_{N \times d} \cdot \underbrace{ \begin{bmatrix} \ & \ & \ & \ & \cdots & \ \\ \ & W & \ & \ & \ & \ \\ \ & \ & \ & \ & \ & \ \\ \end{bmatrix} }_{N \times m} \right ) w - y \right\|^2 \]
Non-linear Example
To illustrate the rank recovery property and the improvement for finding a unique solution to the least squares problem, we consider a simple example below.
Show the code
import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import lstsq, matrix_rank
# Set random seed for reproducibility
np.random.seed(42)
# Parameters
N = 10 # Number of samples
d = 5 # Dimension of input u
m = 10 # Increased dimension for W
# Generate random input data U (d x N)
U = np.random.randn(d, N)
# True weight matrix W_true (d x d)
W_true = np.random.randn(d, d)
w_true = np.random.randn(d)
# Generate nonlinear output to test with
y_linear = (np.cos(U.T @ W_true)) @ w_true
# Initialize random model weight matrix W (d x m)
W = np.random.randn(d, m)
Z = U.T @ W
rank_Z = matrix_rank(Z)
sigma = np.sin
Z_nonlinear = sigma(Z)
rank_Z_nl = matrix_rank(Z_nonlinear)
w_linear, residuals_linear, _, _ = lstsq(Z, y_linear, rcond=None)
w_nonlinear, residuals_nl, _, _ = lstsq(Z_nonlinear, y_linear, rcond=None)
# Check reconstruction error for each case
error_linear = np.linalg.norm(Z @ w_linear - y_linear)
error_nonlinear = np.linalg.norm(Z_nonlinear @ w_nonlinear - y_linear)
# Comparison of Reconstruction Errors
labels = ['Linear Least Squares', 'Non-linear Least Squares']
errors = [error_linear, error_nonlinear]
plt.figure(figsize=(5,5))
bars = plt.bar(labels, errors, color=['skyblue', 'salmon'])
plt.ylabel('Reconstruction Error')
# Annotate bars with error values
for bar in bars:
height = bar.get_height()
plt.annotate(f'{height:.4f}',
xy=(bar.get_x() + bar.get_width() / 2, height),
xytext=(0, 3), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
plt.ylim(0, max(errors)*1.2)
plt.show()
plt.figure(figsize=(5,5))
ranks = [rank_Z, rank_Z_nl]
labels_rank = ['Z (Linear)', 'Z_nonlinear (Non-linear)']
bars_rank = plt.bar(labels_rank, ranks, color=['lightgreen', 'gold'])
plt.ylabel('Matrix Rank')
# Annotate bars with rank values
for bar in bars_rank:
height = bar.get_height()
plt.annotate(f'{int(height)}',
xy=(bar.get_x() + bar.get_width() / 2, height),
xytext=(0, 3), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
plt.ylim(0, m + 1)
plt.show()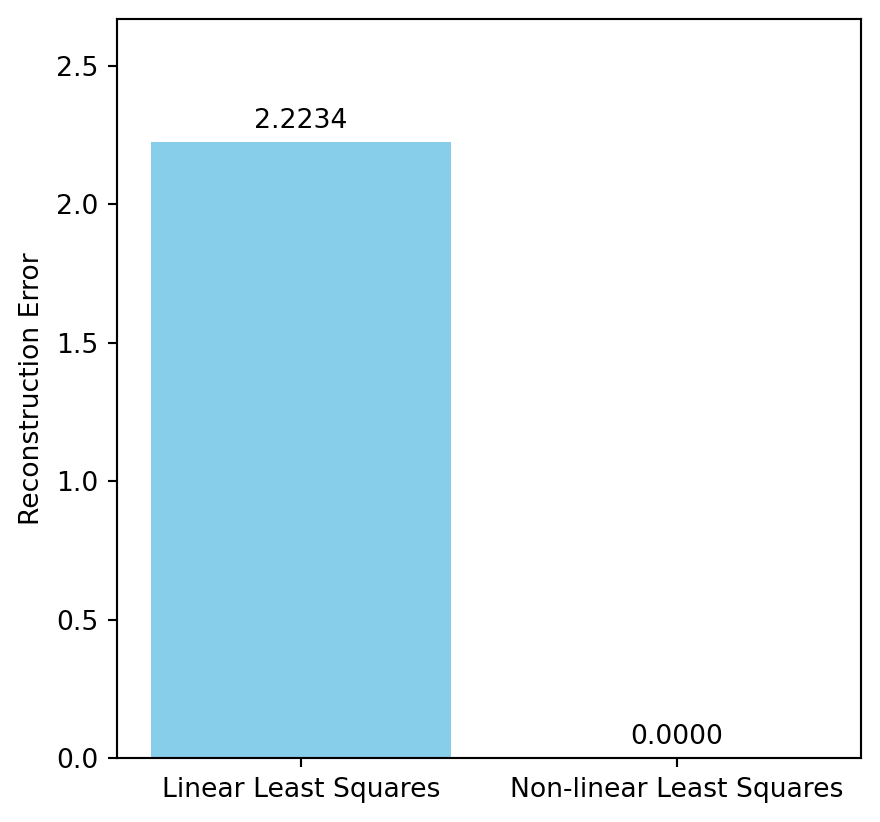
Notes on Scaling
The \(W\) matrix will scale up in \(O(N^2)\) so that with more data samples it can become too large to handle well. The problem however can be solved with a random \(w\) and with \(W\) alone under these conditions. A lower rank \(W\) could help under conditions where the size of \(N\) is large.
\[ W = Q Z^T \]
where \(Q\) is a matrix of orthonormal columns and \(Z\) is a matrix of size \(d \times N\). In this case the product \(U^TW\) for any particular sample \(u_i\) will be giben by \(\sigma((u_i^TQ)Z^T)\). This lower rank matrix leads to the topic of convolutional neural networks (CNNs) which make extensive use of a reduced rank matrix. The benefit is that it can improve the computational speed by exploiting a sparse structure in the matrix \(W\).
This becomes more important when the layers of a SLP are combined into a deep neural network (DNN).
\[y = R(u; \theta) = w^T \sigma(W^{(L)} \sigma(W^{(L-1)} \cdots \sigma(W^{(1)}u + a^{(1)})) + a^{(L-1)}) + a^{(L)}\]
where \(L\) is the number of layers in the network. This is a chain of affine transformations followed by non-linear activation functions and can be expensive to compute in the case where \(N\) is large.
Convolutional Neural Networks (CNNs)
A convolutional neural network makes use of a matrix operator that produces the same result as a discrete convolution.
Convolution Operator
The 1D convolutional operator \(\ast\) in the discrete case is defined as:
\[ (f \ast g)[n] = \sum_{m=-\infty}^{\infty} f[m]g[n-m] \]
In the case of a 2D convolution, the operator is defined as:
\[ (f \ast g)[n,m] = \sum_{i=-\infty}^{\infty} \sum_{j=-\infty}^{\infty} f[i,j]g[n-i,m-j] \]
It is also an operation defined in the continuous domain as:
\[ (f \ast g)(x) = \int_{-\infty}^{\infty} f(y)g(x-y)dy \]
The operation is one that is fundamental to mathematics and shows up in many different applications including, signal processing, image processing, control theory, probability theory, solutions to ordinary and partial differential equations where it is known as the Green’s function, and in the solution of integral equations. Another such home that is has found is in deep learning. The convolution has some intuitive properties that make it useful in any system that is linear and time/shift invariant (LTI).
Properties of Convolution
- Linearity: \(f \ast (\alpha g + \beta h) = \alpha f \ast g + \beta f \ast h\)
- Commutativity: \(f \ast g = g \ast f\)
- Associativity: \(f \ast (g \ast h) = (f \ast g) \ast h\)
Rather than explain convolution at length here, the interested reader is encouraged to look at the Convolution Wikipedia page for some excellent properties and visual examples to build intuition.
In the context of image and data processing, the convolution is closely related to a correlation filter, the two only differe by a rotation of 180 in the convolutional kernel (the function being convolved with the input). This is an important consideration when it comes to working with learned convolutional kernels, since they can be equally interpreted as correlation filters.
Another important property to know is that the convolution operation has a close relationship with the fourier transform. The convolution in the spatial domain is equivalent to a pointwise multiplication in the frequency domain. This is known as the convolution theorem:
\[ \mathcal{F}(f \ast g) = \mathcal{F}(f) \cdot \mathcal{F}(g) \]
When it comes to computing large convolutions for two function \(f(x)\) and \(g(x)\), the convolution theorem can be used to compute the convolution in the frequency domain, which is much faster than the spatial domain.
\[ f \ast g = \mathcal{F}^{-1}(\mathcal{F}(f) \cdot \mathcal{F}(g)) \]
For more details with visual explanations, another good resource is the UBC CPSC 425 course on Computer Vision with slides from Lecture 3b and Lecture 4.
Convolution in CNNs
A convolutinal neural network (CNN) is a type of neural network where the linear mapping involves a convolution operation instead of a dense weight matrix \(W\). The goal of this section is to define the 2D discrete convolution and show how it can be expressed as a sparse matrix.
Single Layer Perceptron (SLP) vs Convolutional Neural Network (CNN)
The single layer of a perceptron given earlier is of the form \(y = w^T \sigma(Wu + a)\), where \(W\) is the weights matrix, \(w\) is the weights vector, \(u\) is the input, and \(a\) is the bias vector. A convolutional network improves the efficiency of computation by exploiting a sparse structure with fewer parameters in the weights matrix. Replacing \(W\) with a sparse convolutional matrix \(C\).
Definition: Convolutional Operation
Let \(\vec{u}\) be the flattened input image \(\mathcal{I}\), and let \(\mathcal{K}\) be the convolutional kernel. The convolutional operation is defined as:
\[ Y[s,t] = \mathcal{K} \ast \mathcal{I} = \sum_{i=-\infty}^{\infty} \sum_{j=-\infty}^{\infty} \mathcal{K}[i,j] \mathcal{I}[s-i,t-j]\]
- \(Y[s,t]\) is the output at position \((s,t)\)
- \(N\) and \(M\) are the dimensions of the kernel \(\mathcal{K}\)
- \(\mathcal{K}[i,j]\) is the element in the \(i\)-th row and \(j\)-th column of the kernel
The kernel slides across the input image, producing a weighted sum at each valid position to give output \(Y\). The indices are clipped from infinity to the correct size depending on the padding, size of kernel, and the stride.
It is a linear operation so that every element of \(Y\) is a linear combination of the input and weights elements, indicating that it can be expressed as a matrix multiplication with the flattened image \(\vec{u}\) and the flattened kernel \(\vec{k}\).
Example: Convolution of a \(2\times 2\) Kernel with a \(4\times 4\) Image
Input Image: \[ \mathcal{I} = \begin{bmatrix} u_{1,1} & u_{1,2} & u_{1,3} & u_{1,4} \\ u_{2,1} & u_{2,2} & u_{2,3} & u_{2,4} \\ u_{3,1} & u_{3,2} & u_{3,3} & u_{3,4} \\ u_{4,1} & u_{4,2} & u_{4,3} & u_{4,4} \\ \end{bmatrix} \]
Kernel: \[ \mathcal{K} = \begin{bmatrix} k_{1,1} & k_{1,2} \\ k_{2,1} & k_{2,2} \\ \end{bmatrix} \]
Output: The output of the convolution will be a \(3 \times 3\) matrix, since the kernel slides over the \(4 \times 4\) image with no padding and a stride of 1.
\[ Y = \begin{bmatrix} y_{1,1} & y_{1,2} & y_{1,3} \\ y_{2,1} & y_{2,2} & y_{2,3} \\ y_{3,1} & y_{3,2} & y_{3,3} \\ \end{bmatrix} \]
Note that the output indexing loses the first and last row and column because there is no padding. In cases with zero padding, then all undefined indices of the input are set to zero when using the convolution formula and reaching undefined indices.
Each element \(y_{s,t}\) of the output is given by: \[ y_{s,t} = \sum_{i=1}^{2} \sum_{j=1}^{2} \mathcal{K}[i,j] \cdot \mathcal{I}[(s+2)-i, (t+2)-j] \]
The addition of \(2\) in the indexing is due to the size of the kernel being \(2 \times 2\) and the choice to index \(y\) starting from \(1\) instead of \(3\) for the case with no padding.
Flatten the Input Image:
Flatten the \(4 \times 4\) image \(\mathcal{I}\) into a column vector \(\vec{u} \in \mathbb{R}^{16}\): \[ \text{flatten}\left(\mathcal{I}\right) = \vec{u} = \begin{bmatrix} u_{1,1} & u_{1,2} & u_{1,3} & u_{1,4} & u_{2,1} & u_{2,2} & u_{2,3} & u_{2,4} & u_{3,1} & u_{3,2} & u_{3,3} & u_{3,4} & u_{4,1} & u_{4,2} & u_{4,3} & u_{4,4} \end{bmatrix}^T \]
Sparse Convolution Matrix:
The convolution operation is expressed as a matrix multiplication: \[ \text{flatten}\left( Y \right) = \mathbf{C} \vec{u} \]
Here, \(\mathbf{C}\) is the sparse matrix representation of the \(2 \times 2\) kernel, with size \(9 \times 16\) (matching the size of the output vector and the input vector). The non-zero entries in each row of \(\mathbf{C}\) correspond to the flattened values of \(\mathcal{K}\).
Looking at the first few entries of the output \(Y\) defines the matrix entries:
- \(y_{1,1} = k_{2,2}u_{1,1} + k_{2,1}u_{1,2} + k_{1,2}u_{2,1} + k_{1,1}u_{2,2}\)
- \(y_{1,2} = k_{2,2}u_{1,2} + k_{2,1}u_{1,3} + k_{1,2}u_{2,2} + k_{1,1}u_{2,3}\)
- \(y_{1,3} = k_{2,2}u_{1,3} + k_{2,1}u_{1,4} + k_{1,2}u_{2,3} + k_{1,1}u_{2,4}\)
\[ \mathbf{C} = \begin{bmatrix} k_{2,2} & k_{2,1} & 0 & 0 & k_{1,2} & k_{1,1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & k_{2,2} & k_{2,1} & 0 & 0 & k_{1,2} & k_{1,1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & k_{2,2} & k_{2,1} & 0 & 0 & k_{1,2} & k_{1,1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & k_{2,2} & k_{2,1} & 0 & 0 & k_{1,2} & k_{1,1} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & k_{2,2} & k_{2,1} & 0 & 0 & k_{1,2} & k_{1,1} & 0 & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \end{bmatrix} \]
Then using this matrix and the flattened input image, a flattened output vector can be computed as $\(\text{flatten}\left(Y \right) = C \vec{u}\).
So the convolution operation gives a matrix that only has \(4\) parameters out of the \(9 \times 16 = 144\) total elements, with most of the entries being zero. This can be highly efficient for compuations in a neural network for spatially invariant features in the input data. The sparse structure of the matrix can also be exploited for efficient computation.
Channels in Convolutional Neural Networks
The data being processed in a CNN can have multiple channels, such as color images with \(3\) channels. The images may also be processed in batches, adding yet another dimension to the input data. For a single image that is size \(\{C,H,W\}\) where \(C\) is the number of channels, \(H\) is the height, and \(W\) is the width, a different convolutional kernel is applied as a mapping from \(C_{in}\) channels to \(C_{out}\) channels. To flatten the input image with channels, the flattened single channels are stacked vertically to form a single column vector.
For \(k\) input channels and \(l\) output channels:
\[ y = \begin{bmatrix} W_{1,1} & W_{1,2} & \cdots & W_{1,k} \\ W_{2,1} & W_{2,2} & \cdots & W_{2,k} \\ \vdots & \vdots & \ddots & \vdots \\ W_{l,1} & W_{l,2} & \cdots & W_{l,k} \\ \end{bmatrix} \begin{bmatrix} u_{c=1} \\ u_{c=2} \\ \vdots \\ u_{c=k} \\ \end{bmatrix} \]
The \(W\) are the individual convolutional kernel maps for each input to output channel. The input is a flattened tensor of size \(k \times H \times W\), and the output is a flattened tensor of size \(l \times H \times W\).
To extend the CNN structure to accept batches, the input data is pooled together into a matrix of flattned input data, where each column is a flattened input image. For a batch size of \(N\), the input data is of size \(N \times k \times H \times W \times N\) and the output data is of size \(N \times l \times H \times W\).
\[ Y_{\text{batch}} = \begin{bmatrix} W_{1,1} & W_{1,2} & \cdots & W_{1,k} \\ W_{2,1} & W_{2,2} & \cdots & W_{2,k} \\ \vdots & \vdots & \ddots & \vdots \\ W_{l,1} & W_{l,2} & \cdots & W_{l,k} \\ \end{bmatrix} \begin{bmatrix} u_{1,c=1} & u_{2,c=1} & \cdots & u_{N,c=1} \\ u_{1,c=2} & u_{2,c=2} & \cdots & u_{N,c=2} \\ \vdots & \vdots & \ddots & \vdots \\ u_{1,c=k} & u_{2,c=k} & \cdots & u_{N,c=k} \\ \end{bmatrix} \]
Deep CNNs
A deep CNN wil chain multiple convolutional layers together, including a non-linear activation function and bias after each later:
\[ y = \sigma(W^{(L)} \sigma(W^{(L-1)} \cdots \sigma(W^{(1)}u + a^{(1)}) + a^{(L-1)}) + a^{(L)} \]
A famous implementation of a deep CNN that broke new ground in the world of image processing is the ResNet architecture (He et al. 2015). The ResNet was able to train very deep networks with hundreds of layers by using skip connections that bypassed one or more layers. Each sequential layer in the architecture is to train a change in the residual rather than the entire output to the next layer.
\[ u_{n+1} = u_n + h \sigma(W_n u_n + a_n) \]
When \(h\) becomes small, this resembles the Euler method for solving ordinary differential equations where \(\frac{du}{dt} = \sigma(W_t u + a_t)\). Where the parameters are also time dependent.